Eynnzerr's Blog

2021-2025 重新出发

0%

《CSAPP》—— Data Lab

发表于 更新于 分类于 ，
本文字数： 10k 阅读时长 ≈ 18 分钟

该篇内容为原博客博文，原上传于2022年4月30日。

话说从寒假开始半摸半读《CS:APP》，但是一直没有写Lab。都说9个Lab是全书的精华，因此深感有必要做一下，所以前阵子抽空先把DataLab做了。虽说是第一个（据说也是最简单的）Lab，却也做的磕磕绊绊，深感自己码力不足。总之最后是完成了，还是写篇博客记录一下，也方便自己日后review。

1分题

1分题基本都是签到题，难度不大。

bitXor
1
2
3
4
5
6
7
8
9
10
/* 
 * bitXor - x^y using only ~ and & 
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) {
  return ~(~(~x&y)&~(x&~y));
}

只使用位与和位非实现位或，运用De Morgan’s laws就行了。

tmin
1
2
3
4
5
6
7
8
9
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
  return 0x1 << 31;
}

返回补码表示的最小数，即0x8000_8000，也即int类型能表示的最小数，也没有什么好说的。

2分题

开始有些技巧性的操作出现了。

isTmax
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
  int i = x + 1; // Tmin,1000...
  x = x + i; // -1,1111...
  x = ~x; // 0,0000...
  i = !i; // exclude x=0xffff...
  x = x + i; // exclude x=0xffff...
  return !x;
}

要求如果x是补码表示的最大数就返回1，否则返回0。
那么我们首先要能识别出补码最大数，并且能将其转化为0x1作为结果。显然0x7fff_ffff就是补码最大数，如何利用允许使用的运算符将其转化为0x1呢？这里就比较tricky了。我们可以取x + 1 + x，如果x是0x7fff_ffff时，将得到0xffff_ffff，即全1。对全1取位反即可得到0，再对0取逻辑非就能得到0x1了。
但这里有一个容易忽略的情形，即当x为0xffff_ffff时，由于溢出，x + 1 + x也能得到同样的结果（我是在btest时才发现这个特例），所以需要排除这个情形，使得只有当x=0x7fff_ffff时才能返回0x1。为此，我们可以不着急对0取逻辑非，而是先再对原来的x+1取逻辑非，再加给取位反后的x + 1 + x。当x为0x7fff_ffff时，这一步多出的操作不会对结果造成任何影响，因为此时x + 1取非后得到的是0，加个0显然不会有影响；但对于x为0xffff_ffff时，x + 1取非后得到的是1，加回去后得到1，再取逻辑非时就变成了0，从而排除了这个例外。

allOddBits
1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  int mask = 0xAA + (0xAA << 8);
  mask = mask + (mask << 16); // mask = 0xAAAAAAAA
  x = mask & x;
  return !(~x & mask);
}

从0开始计位，若x所有奇数位都为1则返回1，否则返回0。
如何提取x的奇数位呢？显然用一个奇数位为1，偶数位为0的mask就行了，但我们不能直接用int mask = 0xAAAAAAAA构造出这个掩码，因为Lab要求整数实验的代码最多使用8位常数，如0xAA，所以我们首先要用0xAA产生0xAAAAAAAA，方法有很多，这里就不再赘述。再用这个mask与x位与，即可在结果的奇数位上对应得到x的奇数位。如何判定x的奇数位是否全为1呢？我们很容易想到如果如此，那么x位反后再与mask位与，应当得到全0，因为一个是奇数位全0，偶数位全1，另一个是奇数位全1，偶数位全0，没有一位是相等的。再对结果取逻辑非就能得到1。而对于不满足的x，检验可知经同样的运算，最终都会得到0。

negate
1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
  return ~x + 0x1;
}

返回x的相反数。只要对补码表示有基本了解，这题应该都是秒过，不再赘述。

3分题

难度更大了。。。

isAsciiDigit
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/* 
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x) {
  // 考察如何使用位运算比较大小->不能直接用算术运算符，但思路依然是可以比较符号位->用位运算凑出符号位改变的临界数
  int sign = 0x1 << 31;
  int compH = ~(sign | 0x39); // 当与小于等于0x39的数相加后，符号位为0；当与大于0x39的数相加后，符号位变为1
  int compL = ~0x30; // 当与大于0x30的数相加后，符号位为0；当与小于等于0x30的数相加后，符号位变为1
  int sign_1 = ((compH + x) & sign) >> 31; // 当符号位为0时，得到sign_1为全0；当符号位为1时，得到sign_1为全1
  int sign_2 = ((compL + x + 0x1) & sign) >> 31; // 这里需要额外加个1，因为当x=0x30时，符号位仍为1，需要加1进位使其变为0.且加1不会对0x30之后的数的结果产生影响
  return !(sign_1 | sign_2); // 这里要用逻辑非来实现或非，因为最后要求的是返回0/1，而sign_1/2位或后仍是32位全0/1整数
}

若x是0~9数字的ASCII码表示，则返回1，否则返回0。
只要我们能比较x同0x30和0x39的大小就行了。如何用位运算比较两个数之间的大小呢？（我不道啊？看了别人的写法才懂）有一种比较tricky的处理方式，虽然这题不给用减法，但我们可以借鉴类似的想法，即自己构造出会使得符号位改变的临界数，再看符号位就行了。具体思路可以看代码注释。

conditional
1
2
3
4
5
6
7
8
9
10
11
12
/* 
 * conditional - same as x ? y : z 
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
  int flag = !!x;
  int mask = ~flag + 1;
  return (y & mask) + (z & ~mask);
}

这里的难点在于如何从x的位级表示获取其一位布尔值，使用逻辑非即可。第一次逻辑非会把0转化为1，非0转化为0，第二次逻辑非会还原为原逻辑值，所以需要2次逻辑非。但我们不能直接用这个一位布尔值，因为要实现选择操作，用一位只能保留原输入的一位，显然是不对的，故还需经一步得到全1和全0，再做与操作。

isLessOrEqual
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  int sign = 0x1 << 31;
  int sign_x = x & sign;
  int sign_y = y & sign;
  int sign_inequal = ((sign_x ^ sign_y) >> 31) & 0x1; // sign_inequal为0x1，表示符号不同；为0则表示符号相同
  int sign_diff = (y + ~x + 0x1) & sign; // y - x 的差值符号，当为0x1<<32时表示y<x，当为全0时表示y>=x。 有错误：当x为负，y为正时有可能溢出，因而不可靠。只有当符号相同时才可靠
  int same_res = !sign_diff;// 符号相同时的结果
  int diff_res = !sign_y;//符号不同时的结果，当y为正数时返回值就为1，否则返回0
  return (sign_inequal & diff_res) + (!sign_inequal & same_res);//符号不同时，即sign_equal为1时，返回diff_res；否则返回same_res
}

比较x,y大小，返回比较结果。
第一眼看，我们也许会想用isAsciiDigit的思路做这题，但这是不行的。因为上一题我们只考虑0x30~0x39这一正数小区间，而现在我们需要考虑整个实数域。用相同的方法处理y为负数时会出现问题。
这时就要回退到一般运算思路，即符号不同正数为大，符号相同看差值符号即可。获取差值时，这里不能直接用’-‘，故用补码方式。
x,y和y-x的符号不难获得，但难点在于如何通过位运算在符号不同时正确选择正的那一个数，思路可参见代码注释。

4分题

这几位更是重量级。

logicalNeg
1
2
3
4
5
6
7
8
9
10
11
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int logicalNeg(int x) {
  return ((x | (~x + 1)) >> 31) + 1;
}

实现逻辑非运算符。要做出这题，首先需要清楚C语言中的右移对于有符号数是算术右移，以及整数中的1000…0000表示最小数而不是表示负零。其次，还是要想办法将位级表示的x的信息用一个比特表示出来，之前我们都是用!!，但这题就是需要我们实现!，故得采取新的思路。想到对于0来说，其原码和补码都是0x0000，符号位相或仍为0；而对于非0数，其源码和补码的符号位必然互补，从而相或时为1，进而就可以区分0和非0数了。最终要求是求反，故再加1即可。
真正实现起来，一行代码即可搞定，但背后的思考过程不是那么容易，你得想到0和非0数各自相反数符号位的差异，才能做出这题。

howManyBits
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
  int b16, b8, b4, b2, b1, b0; // 必须提前声明，否则dlc检查时会报错
  int sign = x >> 31; // 提取符号位，sign为全1或全0
  x = (sign & ~x) | (~sign & x); // 这一步是为了方便处理负数。对负数取反，将找0转化为找1，这样对于正负数就可以统一处理了
  //经上一行操作后，x符号位总为0，故算术右移不会造成影响
  b16 = !!(x >> 16) << 4; //考察高16位是否有1，若有，b16得16，否则得0，至少需要16位。
  x = x >> b16; //若高16位有1，则将x右移16位。对于b16=16，此为向左缩小搜索范围；对于b16=0，此为向右增大搜索范围
  b8 = !!(x >> 8) << 3; //考察高8位是否有1，若有，b16得8，否则得0，至少需要位数再加8位
  x = x >> b8; //继续缩小范围，考察高4位。下面以此类推。
  b4 = !!(x >> 4) << 2;
  x = x >> b4;
  b2 = !!(x >> 2) << 1;
  x = x >> b2;
  b1 = !!(x >> 1);
  b0 = x >> b1; // 最高两位是11时，所需位数还得加1
  return b16 + b8 + b4 + b2 + b1 + b0 + 1; // 符号位必定占一位
}

求用补码表示x至少需要几位。思路很好想，符号位必定占一位，剩下的从左往右找第一个有效位(正数是1，负数是0)，其与之后剩下的位都是需要的位。但是代码实在写不出来，就copy别人的代码了。
实际上代码的思路也很简单，就是在这串32位比特上做二分搜索（还能这样，艹），找到第一个有效位,同时统计比特数量。
这里还有一个小插曲，即使用的临时变量都必须在函数的一开始提前声明，不能在使用时才声明并初始化，否则dlc检查时会报错，说你没有声明变量。不太清楚原因。

floatScale2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  int exp = (uf & 0x7f800000) >> 23; //exp低23位表示原数的阶码
  int sign = uf & 0x80000000; // sign最高位为原数符号位，其余位全为0
  if (exp == 255) return uf; // 无穷或NaN
  if (exp == 0) return sign | (uf << 1); // 非规格数
  if (++exp == 255) return sign | 0x7f800000; // 溢出，返回无穷大
  return (exp << 23) | (uf & 0x807fffff); // 规格数且无溢出
}

实现2*f。与前面的题相比，这题其实不难，只要认真读了书，知道浮点数的表示方法就能做出来。
若为规格数，直接阶码加1即可。但若阶码加1后变为全1，则返回的应是对应符号的无穷大。
若为非规格数，则直接左移1位并补上符号位即可。这是因为当非规格数的小数字段最高位为0时，直接左移1位仍表示为非规格数，且小数字段因左移而乘以2，自然得到了结果
当小数字段最高位为1时，左移1位会导致阶码变为0x1而成为规格数。但对规格数而言，0x1阶码与非规格数表示的指数相同，都为1-Bias。且虽然小数最高位看似丢失了，但规格数表示的尾数本身就是1+f，与非规格数的尾数f相比，相当于把最高位的1表示成十进制的0.5乘以2得到的1单独提取了出来，其余位左移自然乘以2。得益于IEEE浮点标准的这种非规格数平滑向规格数过渡的设计，我们这里处理非规格数也简单很多，不需要担心溢出。
若为无穷大和NaN，直接返回原数即可

floatFloat2Int
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  int exp, E, tail, sign;
  if (!(uf & 0x7fffffff)) return 0; // 当uf为0，-0时，直接返回0即可。注意这个-0容易遗漏

  exp = (uf & 0x7f800000) >> 23;
  sign = uf & 0x80000000;
  tail = (uf & 0x007fffff) | 0x00800000; // 由于之后的代码会排除非规格数，故对规格数而言，真实的小数表示为尾数+1，这里与0x00800000相或就是为了加上小数点前的1

  E = exp - 127; // E表示由阶码复原得到的真实指数，注意E > 31时，必定在左移时覆盖掉符号位，所以会溢出。此时也包括了NaN和INF（E=255-127必然大于31）
  if (E > 31) return 0x80000000;
  if (E < 0) return 0; // 直观来理解，对于始终小于2的尾数，当E < 0时，相当于至少除以2，所得一定是个小于1的小数，故取0。非规格数也在这里被排除

  // 0 <= E <= 31时，依然有可能发生溢出，故需要做甄别并排除
  // 开始左移/右移。当E > 23时，说明乘法后所有小数点后的原尾数位都移到了小数点前，此时结果为一个整数，故直接左移即可。 当E < 23时， 说明乘法后仍含有小数部分，
  // 则转为Int时直接丢弃这些小数部分即可，对应的操作就是右移
  tail = (E > 23) ? tail << (E - 23) : tail >> (23 - E);
  // 原来是按位表示的1+小数，故对E>23来说，一开始乘2时会先移动小数点，故不会改变作为Int的各位数值。只有当超过23部分的E会导致数值开始乘2，即左移
  // 而对于E<23来说，无论如何都只会改变小数点而不改变数值，因而不会左移。但因为此时含有小数，故权值不是从0而是从某个负数开始，因而各位上的权值对应都会衰减，本应是右移23位来对上小数
  // 的权值，但因为有乘E次2的操作，每次乘2都会使权值对应升高1位，故会抵消E次右移操作，最终效果就是右移23-E位。同时在右移的过程中，还舍去了小数的信息。
  // 统一的解释：因为小数从左向右的权值是从-1开始的，而不是从0开始的，故对于原小数的位级表示，应首先右移23位来对上正确的权值(<<-23 or >>23)。
  // 但因为有乘E次2的操作，每次乘2都会使权值对应升高1位，故会抵消E次右移操作，最终效果就是右移23-E位(<<E-23 or >> 23-E)。同时注意在右移的过程中，还会舍去小数的信息。
  return sign ? -tail : tail; // 保留原符号
}

实现float到int强制类型转换。这题也没写出来，copy了网上代码，代码解释看注释就行。

floatPower2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsigned value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
  int exp = x + 127; // 加上bias得到位级表示的阶码
  // 阶码的范围是00000000~11111111，超出这个表示范围时，对应0(全0)和INF(0111_1111_1000_0...0)
  if (exp <= 0) return 0; // 极小数，当做0
  if (exp > 0xff) return 0x7f800000; // INF 
  return exp << 23;
}

实现2的幂次方运算。这题简单一点，首先由x加上bias得到对应浮点数的阶码。由于2的幂符号位为0，尾数也为全0，故再对阶码移位到浮点数对应的位置即可。注意要排除极小数和无穷，即超过阶码表示的数。

结果

这里有个小插曲，编译btest时提示不兼容的gcc。这是因为我的机器是x86-64，但Lab的makefile中添加了-m32参数，而我缺少在64位机器编译32位程序的库。这里可以选择修改makefile，把这个参数删去或者改为-m64，或者安装需要的库，有gcc-multilib和module-assistant。
测试结果如图。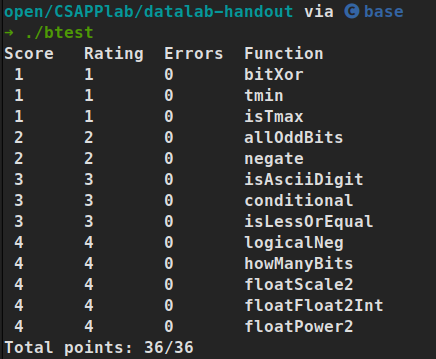
lab_1_result.png

碎碎念

从这个学期开始，我一直处于一种浑浑噩噩的状态，课内没学好，加权卷不上去，课外的知识也进度缓慢（包括但不限于CSAPP只读到了第四章，计算机视觉半熟不熟，几个月没写安卓）。最近看了许多大牛学长的博客和他们的经历分享，收获了很多，还是希望能向强者靠拢。开始做CSAPP的lab，也算是自己挣脱摆烂状态的一次尝试。希望自己能继续努力，保持学习吧！